湖南大学智能车辆课题组联合清华大学、加州大学伯克利分校等研究团队,在多智能体协同控制领域取得重要进展。相关研究成果已发表于《International Journal of Robust and Nonlinear Control》。该论文在 2025 年第二季度中国作者发表的文章中表现卓越,影响力位居前列,荣获 2025 年第二季度“Wiley 威立中国高贡献作者奖”。

作为支撑群体调度与高效运行的核心技术,多智能体控制(Multi-Agent System Control)在自动驾驶车群、空中无人机集群、移动机器人协作、仓储自动物流、星链导航定位等诸多领域中展现出广阔的应用前景,近年受到学术界与工业界的广泛关注。现有研究多聚焦于“线性模型(Linear Model)”的多智能体控制方法,这类方法通常依赖于系统动力学可线性化或线性近似的前提,以通信拓扑矩阵的特征值分解为核心技术手段。然而实际应用中,许多对象本身具有显著的“非线性(Nonlinear)”特性,采用线性版本的多智能体控制技术,不免导致闭环动态性能下降、系统稳定性无法保证等难题。
如何实现“通用”非线性对象的多智能体控制,这是学术界和工业界持续关注的核心问题。分布式模型预测控制(Distributed Model Predictive Control, DMPC)是当前学界的一类主流方法。但该类控制器的设计高度依赖在线优化求解,即每个控制周期内都需利用当前状态预测未来行为,并优化计算最优控制序列。当优化问题复杂度较高时,在线计算的开销十分大,难以满足实际工程的实时性要求。
针对这一难题,研究团队提出一类具有“普遍适用性”的分布式滑模控制(Distributed Sliding Mode Control, DSMC)方法,能够显式支持各类通信拓扑结构,具有良好的非线性处理能力和问题规模可拓展性。具体而言,DSMC 方法具有以下创新:(1)首次定义了结构化拓扑函数(Topologically Structured Function),实现对任意多智能体滑模面及趋近律的抽象建模与统一表达,仅要求通信拓扑结构包含一个有向生成树;(2)首次提出了多智能体控制律设计的拓扑矩阵对消机制,实现了高阶系统的阶数降维缩减,极大简化了滑模变结构控制律的设计难度。这一方法除了具有良好地非线性适用性之外,在提升系统鲁棒性、拓扑适应性与工程实时性方面展现出显著优势,为多智能体系统的非线性协同提供了一条全新的工程化路径。
结构化拓扑函数
对于任意向量集合 {zi}1N,其中 zi∈ Rn,定义节点 i 的拓扑结构函数为
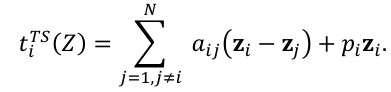
其中,Z = [z₁ᵀ, z₂ᵀ, …, zNᵀ]ᵀ ∈ Rⁿᴺ 表示所有节点状态的堆叠向量。系数 aij= 1 表示节点 i 能够收到来自节点 j 的信息,否则 aij= 0;pi= 1 代表节点 i 能够接收到来自领导者(Leader)的信息,否则 pi= 0。以此为基础,任意多智能体系统的拓扑结构函数可表示为

其中,𝓛为MAS的拉普拉斯矩阵(Laplacian matrix),𝒫为牵引矩阵(Pining matrix),⊗表示克罗内克积,𝐼ₙ为n阶单位矩阵。证明可知:如果𝓛+𝒫是非奇异矩阵,多智能系统的拓扑结构函数是一个同构(Isomorphism),也就是说仅要求通信拓扑结构包含一个有向生成树。
拓扑滑模面及拓扑趋近律
对于 N 个节点的非线性多智能体系统,定义第 i 个节点的滑动变量为
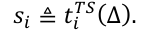
其中,Δ ≜ [δ₁, δ₂, ..., δₙ]ᵀ。据此定义滑动模态向量为
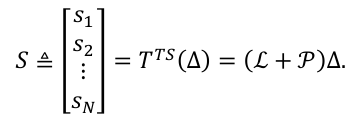
由于拓扑结构函数 TTS(·)是同构,因此
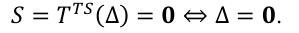
该设计将 N 个高阶动态系统映射为N维滑动变量空间,TTS同构性的存在进一步将复杂的多智能体一致性问题转化为滑模面上的低维控制问题,显著降低了设计难度。
进一步设计节点i的拓扑趋近律为
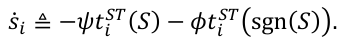
其中,ψ 和 φ 是调节参数。定义 sgn(S) ≜ [sgn(s₁), …, sgn(sN)]ᵀ,其中 sgn(·) 是符号函数。结合所有节点,我们得到了紧集形式的趋近律:
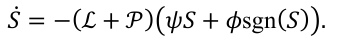
拓扑矩阵的对消机制
拓扑矩阵的对消机制是 DSMC 方法的核心创新,这是降低多智能体控制律阶次的关键。考虑滑动模态向量导数方程:
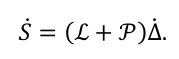
将其代入趋近律可得:
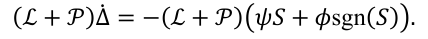
由于组合矩阵𝓛+𝒫具有非奇异特性,可通过矩阵求逆实现精确对消,从而导出:
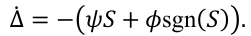
很明显:该组合矩阵𝓛+𝒫的非奇异性是本方法的关键,其保证了控制律对通信拓扑结构的普遍适用性,且能够兼容各类不同的拓扑场景。对于节点 i 的分布式实现,控制量可解耦为:
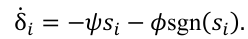
通过联立节点动力学模型和中间误差变量的微分关系,最终可推导出 DSMC 的控制律。该对消机制突破了传统 SMC 方法对特定通信拓扑结构的依赖,为非线性多智能体系统在复杂通信环境下的一致性控制提供了新思路。
非线性多智能体系统验证
为验证所提方法的有效性,本文选用独轮车模型(unicycle model)作为研究对象。在三种不同的通信拓扑结构下,独轮车系统应形成如下的编队形式:
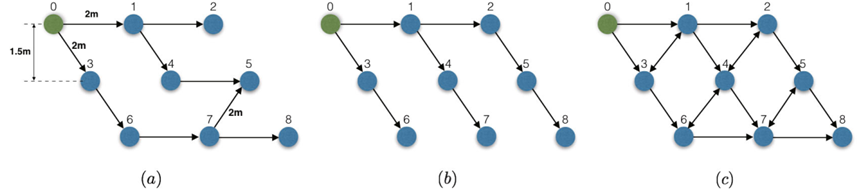
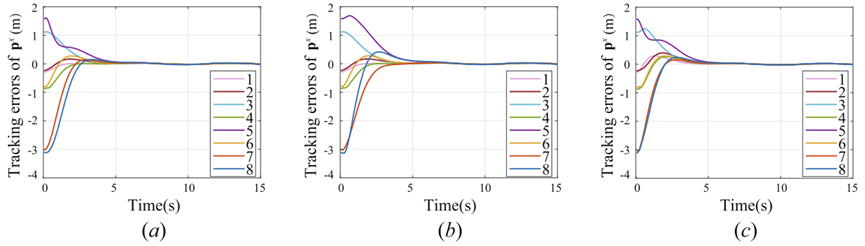
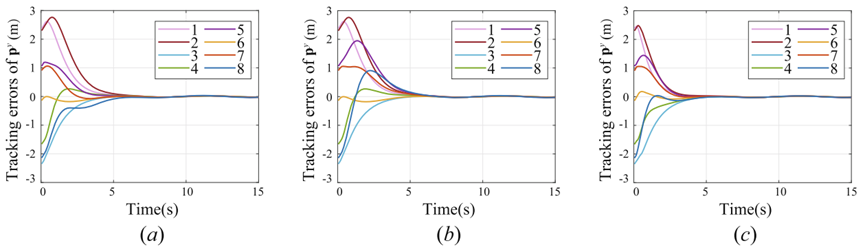
在所设计的多智能体实验中,设定领导者在指定位置沿圆轨迹运动,其余跟随者从随机初始位置出发,在实现期望编队形式后,能够准确跟踪领导者的圆周轨迹。测试结果如下图所示:
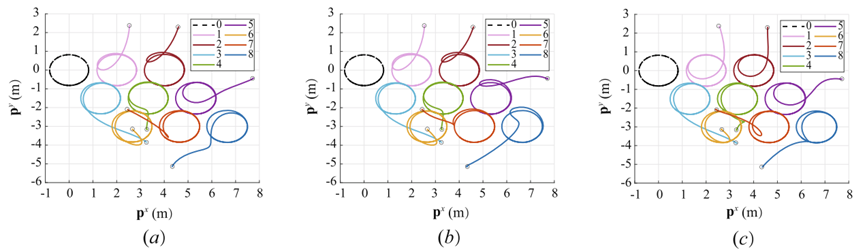
测试结果表明,在这三种不同的通信拓扑结构之下,所有跟随者均能够到达预定位置,并在保持理想编队结构的前提下,实现沿圆轨迹的协同运动,且所有跟随者的跟踪误差能够快速收敛。
总结
综上所述,本文首次提出了一种具有“普适性”的分布式滑模控制(Distributed Sliding Mode Control, DSMC)方法。该框架适用于典型非线性对象,且仅要求通信拓扑结构包含一个有向生成树。所提出的拓扑结构函数(Topologically Structured Function)恰好可以对消拓扑滑模面及拓扑趋近律,极大简化了多智能体滑模控制律的设计难度。除了有效降低控制律的阶次之外,DSMC 方法具备良好的系统鲁棒性、拓扑适应性与工程实时性。这一研究为非线性系统的多智能体控制开辟了全新的路径,具有较好的工程应用潜力。
参考文献
[1] Wu Y, Dong H, Bian Y, Zhao F, and Li S.E. Distributed Sliding Mode Control for Nonlinear Multi-Agent Consensus[J]. International Journal of Robust and Nonlinear Control, 2025, 35(14): 5871–5885.
[2] Wu Y, Li S.E., Cortés J, and Poolla K. Distributed sliding mode control for nonlinear heterogeneous platoon systems with positive definite topologies[J]. IEEE Transactions on Control Systems Technology, 2019, 28(4): 1272–1283.
[3] Wu Y, Li S.E., Zheng Y, and Hedrick J.K. Distributed sliding mode control for multi-vehicle systems with positive definite topologies[C]//2016 IEEE 55th Conference on Decision and Control (CDC). IEEE, 2016: 5213–5219.
[4] Zheng Y, Li S.E., Li K, Borrelli F, Hedrick K. Distributed Model Predictive Control for Heterogeneous Vehicle Platoons under Unidirectional Topologies[J]. IEEE Transactions on Control System Technology, 2017, 25(3): 899–910.
[5] Li K, Bian Y, Li S.E., Xu B, Wang J. Distributed Model Predictive Control of Multi-Vehicle Systems with Switching Communication Topologies[J]. Transportation Research Part C, 2020, 118: 102717–102735.


